© Mislav Predavec, November 2008.
Last Revised: 28/Mar/23.
Mathodica IQ test is a tool for measuring human logic and analytic abilities. Although based on mathematics and it´s methods it is suitable for inductive and constructive reasoning. The fee is 40(€,$,CHF) in cash or 50(€,$,CHF) by bank transfer (hover over email), NO PAYPAL. Answers may be sent by e-mail or by mail with the fee enclosed on address: Mislav Predavec, Jakova Gotovca 2, 10000 Zagreb, Croatia. The certificate of this test is now available in electronic 20(€,$,CHF) or paper 50(€,$,CHF) form. Official score issued by this certificate is average score of first score and the best score. A current score list and norm can be found on the link provided. The raw score follows instantly. This test is currently accepted as an entrance exam by Milenija, Tetra and GenerIQ societies. E-mail: predavec@gmail.com
* Find all values XYZ so that XY ´ Z = YZ where X,Y > 0.
* A human plays tic-tac-toe game against the computer. What is the probability for human to win if he plays first and plays his best moves and
computer plays randomly? Express your answer as a fraction reduced to the lowest common denominator.
* What is the minimum number of people sufficient to ensure that among them exists a group of 3 people which know each other or a group of 3
people which are not familiar.

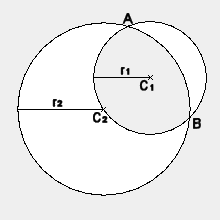
* Find the distance between A and B where circle (C2,r2) intersects circle (C1,r1), center C2 of circle (C2,r2) lies on circle (C1,r1) and r2<2r1.
* What is the minimum number of angles (in whole degrees and positive) sufficient to bring into equality every angle from 1 to 360 (in whole
degrees) on one of its side and another side where each of those angles can be added, subtracted or omitted? Below is an example of 3 angles -
1, 2 and 7 that bring into equality every angle between 1 and 10.
1 = 1; 2 = 2; 3 = 2 + 1; 4 = 7 - 2 - 1; 5 = 7 - 2; 6 = 7 - 1; 7 = 7; 8 = 7 + 1; 9 = 7 + 2; 10 = 7 + 2 + 1;
* How many different umbrellas can be made of 7 colours of spectrum? Any 2 colour patterns which can be made mutually to coincide by the
rotation are considered as indistinguishable.
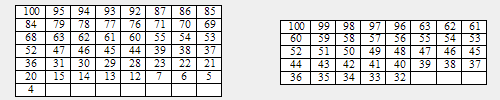
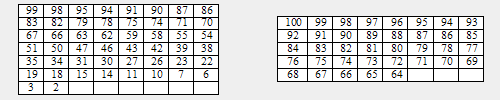
* A mathematician wrote down numbers on 7 tables. He gave those tables to his brother and asked him to imagine a number between 1 and 100
and to give him back only tables where imagined number exists. His brother did so and gave him back 2 tables shown below. The mathematician
took a glimpse on these tables and guessed that number instantly. What number imagined mathematician´s brother?
* Find the lowest and the highest 8 digits number ?4?3?2?1 dividable by 3, 7 and 11 where its 4 digits are already given.
* Fill areas of 2-dimensional young blossom with numbers from 1 to 24 so that the sum in each of his 7 round petals is equal to 82.

* Find the angles from fifth item so that their maximum angle is the lowest possible.
* What is the sum of the infinite series n/(n+1)2+ n2/(n+1)3 + n3/(n+1)4 + ... where n is natural number?
* Find exact lengths of edges a, b and c of a cuboid if its volume is 4, surface area of its 6 rectangles 20 and the sum of lenghts of its 12 edges 24.
* Explorers found remnants of an ancient civilization which existed for millions of years before humanity. Among those artifacts were notes about
its custom and 1.000.000 pyramids of stars as symbols of power of its sovereigns. First ruler proclaimed one star his as a symbol of his reign.
Second ruler proclaimed another 4 stars his, third proclaimed another 10 stars his and so on... Every further dynast proclaimed as much new
stars his as he need to build a pyramid of them a stage taller than previous one. How many entirely different stars sovereigns proclaimed theirs?
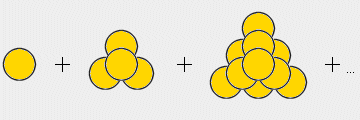
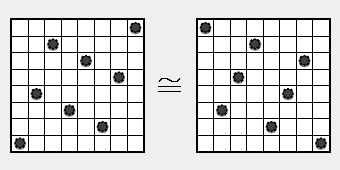
* The mathematician from seventh item gave the tables to his brother once again and asked him to imagine a number between 1 and 100 but this
time to give him back only tables where imagined number doesn´t exist. His brother did so and gave him back 2 tables shown below. The
mathematician now took a glimpse on these tables and guessed that number instantly. What number imagined mathematician´s brother this time?
Draw 3 tables with numbers which didn´t appear in seventh item and this item.
* Find all 4 solutions (x, y, z) in set of integers for system of equations x + y + z = 3 x3 + y3 + z3 = 3.
* How many different ways can be arranged 8 mutually "non-attacking" rooks of black colour on the chess board with no black squares? Any
2 rooks and any 2 arrangements which can be made mutually to coincide by the rotation of the board are considered as indistinguishable.
* In a group of 17 people 11 are non-smokers. What is the probability that among 7 randomly chosen people from this group exactly 3 are
smokers? Express the solution as the nearest whole percent.
* Is there a way to fill areas in ninth item so that the sum in each petal is equal and less than 82? Yes / No
If there is a way, what is the smallest such sum?
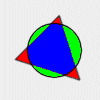
* What is the maximum number of completely bounded areas not further subdivided that can be obtained by the construction of three circles, a
triangle and simple quadrilateral mutually intersecting? Construction of mutually intersecting circle and triangle below produces a maximum of 7.
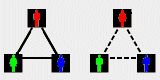
* Members of GenerIQ society were abducted by aliens and imprisoned in flying saucer. Aliens decided to test their intelligence with a challenging
game of guessing a color of the tape glued on the forehead of each member which can be red, green or blue. They were told that all of them will
be settled down in a circle around a big round one-way mirror with small gaps for foreheads so that every member can see only foreheads of all
other members but not his own and called over one by one in randomly order every member having an opportunity to guess a colour of the tape
on his forehead when his time comes. If a member guess a colour of the tape on his forehead he will be released otherwise he will be taken by
aliens to their domicile planet as a slave. Before this procedure they were allowed to confer about the best strategy which will bring them the
greatest chance for liberation of as many members as possible. Once they agree the procedure will start. They were warned also that any try of
cheating like giving signs by gathering a forehead or telling anything else except red, green or blue when they are asked about the colour of the
tape on their foreheads will result in permanent slavery of all members. The members of GenerIQ, being very smart, found out the best strategy.
Describe detaily that best strategy. What is the probability that all members of GenerIQ society were released?
* Find all uknowns
which satisfie the following equation![]() .
.
* Find the limit whom converges a sequence
![]()